Revisiting the Platonic Representation Hypothesis: An Aristotelian View
The Platonic Representation Hypothesis claims that as models scale, their representations across architectures and modalities (vision, language, video) increasingly converge. We revisit this claim and show that widely used similarity metrics can be systematically inflated by model scale (width and depth). After correcting for these effects with a permutation-based calibration, a more nuanced picture emerges: global spectral “convergence” mostly disappears, while local neighborhood relationships remain robust.
This motivates our refined takeaway:
The Aristotelian Representation Hypothesis
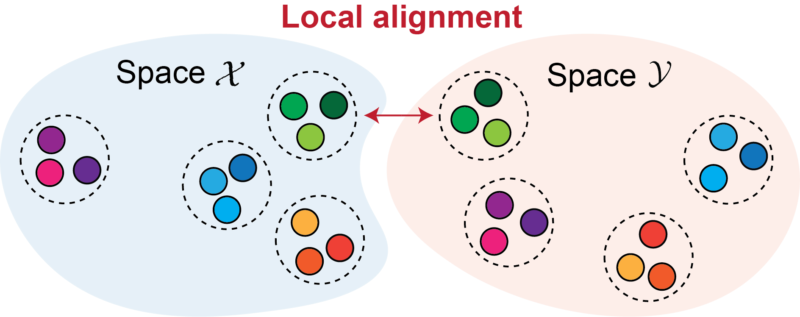
Neural networks, trained with different objectives on different data and modalities, are converging to shared local neighborhood relationships.
In short, models increasingly agree on who is near whom, even when global geometry does not necessarily align.
What is the Platonic Representation Hypothesis?
The Platonic Representation Hypothesis posits that as neural networks become more capable, their learned representation spaces converge toward a shared statistical model of reality. In practice, this idea is tested by measuring representational similarity across model families and modalities and checking whether similarity increases with model scale.
But there is a catch: measuring “representation similarity” is trickier than it looks, and some popular metrics can produce higher scores even when two representation spaces are unrelated.
Why similarity scores can mislead at scale?
Ideally, a representational similarity score should capture only how similar two spaces are, and remain comparable across model pairs and across different metrics. In practice, we find two pervasive confounders:
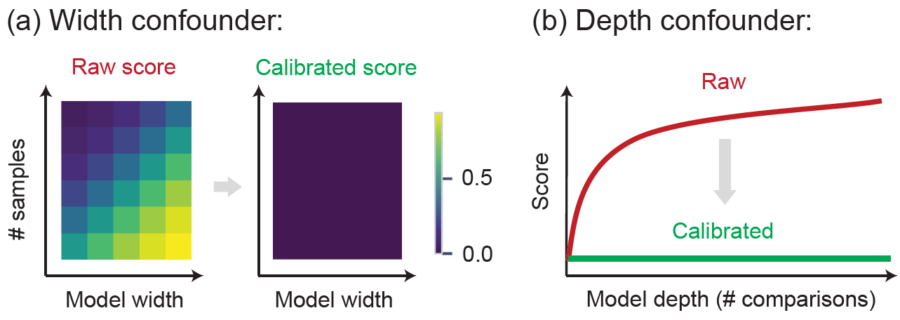
- Width confounder: increasing embedding dimensionality (relative to sample size) can inflate similarity scores, creating non-trivial “chance similarity”.
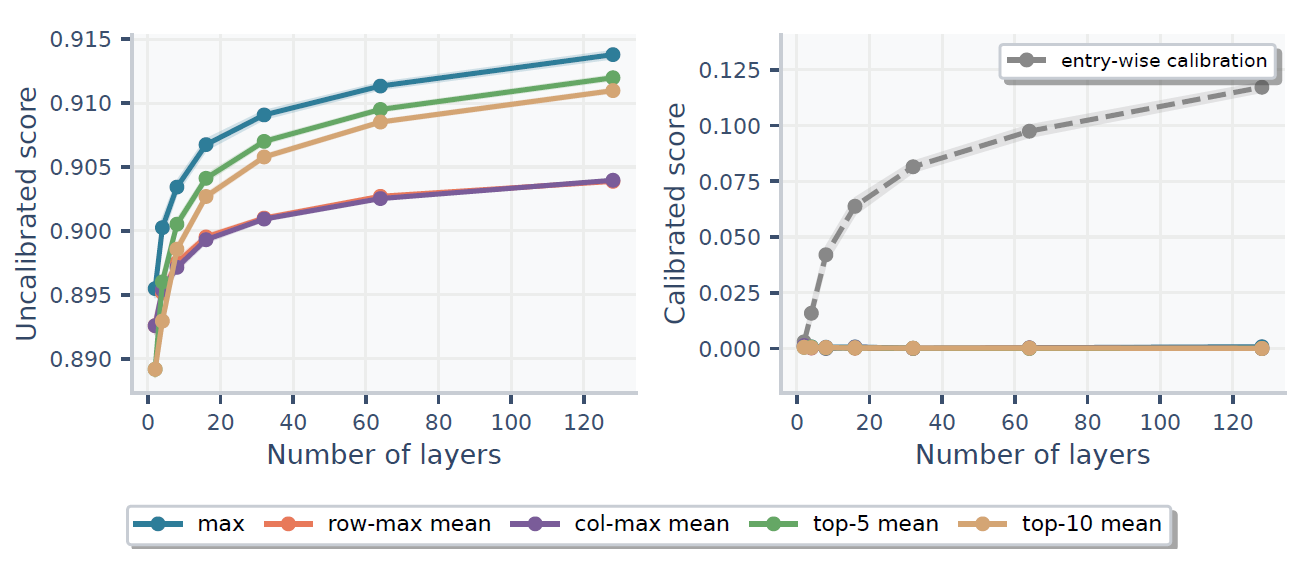
- Depth confounder: common reporting practices search over many layer pairs and summarize with a max / top-k aggregate. The more comparisons you make, the higher the expected maximum becomes, even under no relationship.
Want to know why? See Section 4 of our paper.
These effects can make larger (wider/deeper) models appear more aligned simply because the measurement baseline shifted. So before concluding “models converge”, we need to fix the baseline.
The fix: permutation-based null calibration
We calibrate any similarity metric by comparing the observed score to an empirical null distribution obtained by permuting sample correspondences. This gives a principled “zero point” for no relationship.
Null-calibration in four steps:
- Choose a significance level α (e.g., 0.05).
- Generate K null scores by permuting sample correspondences and recomputing the same similarity metric.
- Use the combined observed + null scores to estimate a right-tail threshold at level α.
- Rescale the observed score into a calibrated effect size (clipped at 0), so “chance similarity” maps to 0.
Details + guarantees: see Section 5 of our paper.
Code snippet
import torch
# pip install calibrated-similarity
from calibrated_similarity import calibrate, calibrate_layers
# Define any similarity function
def cka(X, Y):
X, Y = X - X.mean(0), Y - Y.mean(0)
hsic_xy = (X @ X.T * (Y @ Y.T)).sum()
hsic_xx = (X @ X.T * (X @ X.T)).sum()
hsic_yy = (Y @ Y.T * (Y @ Y.T)).sum()
return hsic_xy / torch.sqrt(hsic_xx * hsic_yy)
# Sample data
X = torch.randn(100, 64)
Y = torch.randn(100, 64)
# Calibrate the similarity
calibrated_score, p_value, threshold = calibrate(X, Y, cka)
print(f"Calibrated: {calibrated_score:.3f}, p={p_value:.3f}")
What changes after calibration?
1) Calibration removes the width confounder.
In controlled experiments where representations are independent, raw scores drift upward as dimensionality grows. After calibration, they collapse to ~0, the desired outcome for “no relationship”.
2) Calibration removes the depth confounder.
If you summarize similarity by searching over many layer pairs (e.g., taking the maximum), uncalibrated summaries inflate with depth. Aggregation-aware calibration fixes this by calibrating the final statistic you report.
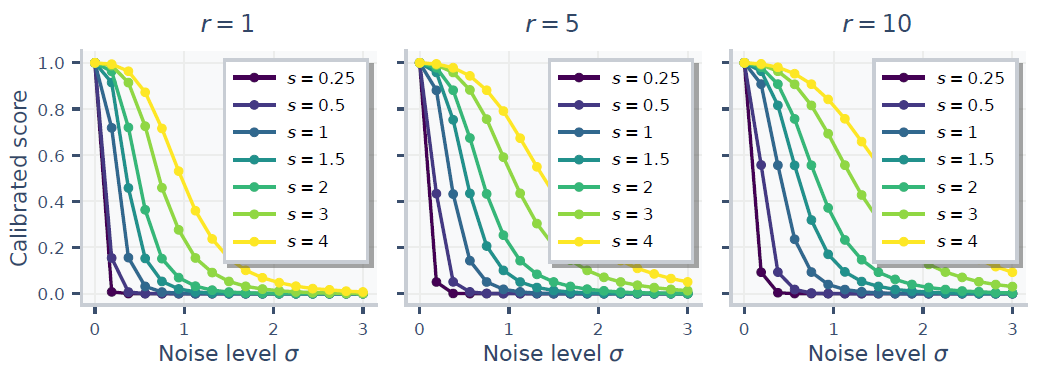
3) Calibration preserves real signal.
When we inject genuine shared structure, calibrated scores remain high when the signal is strong and degrade smoothly as noise increases, i.e., we remove confounds without washing out meaningful alignment.
Now the key question: does the Platonic convergence story still hold after calibration?
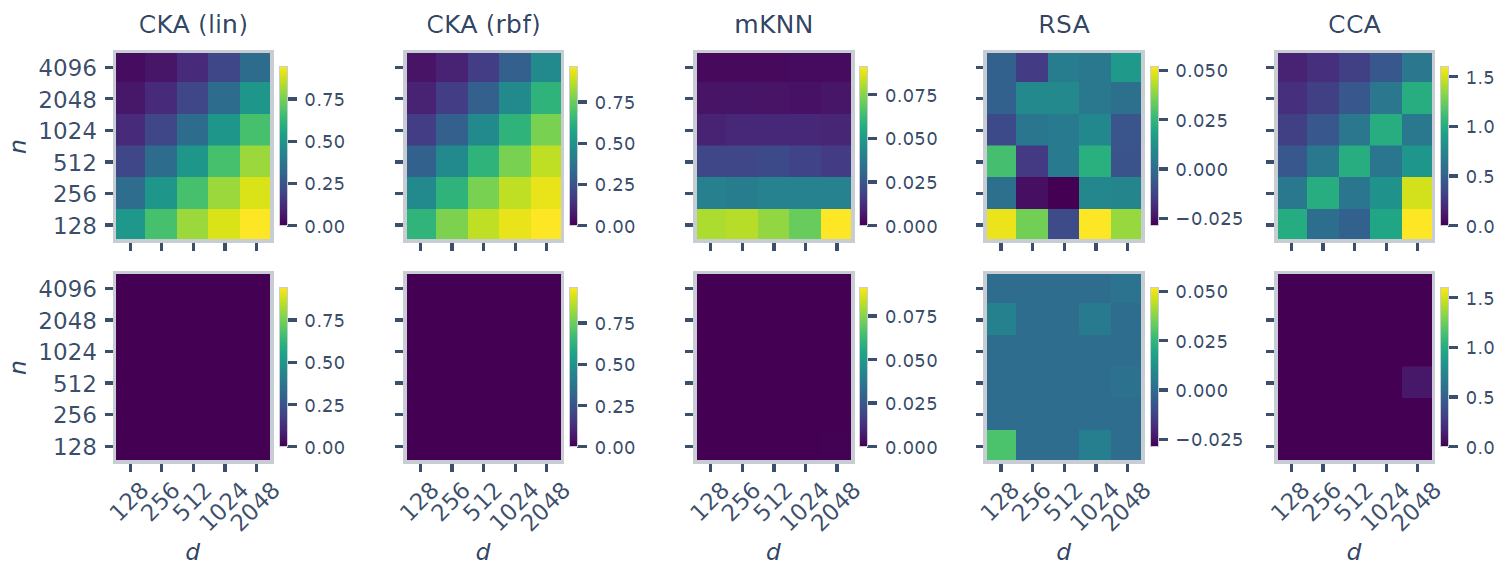
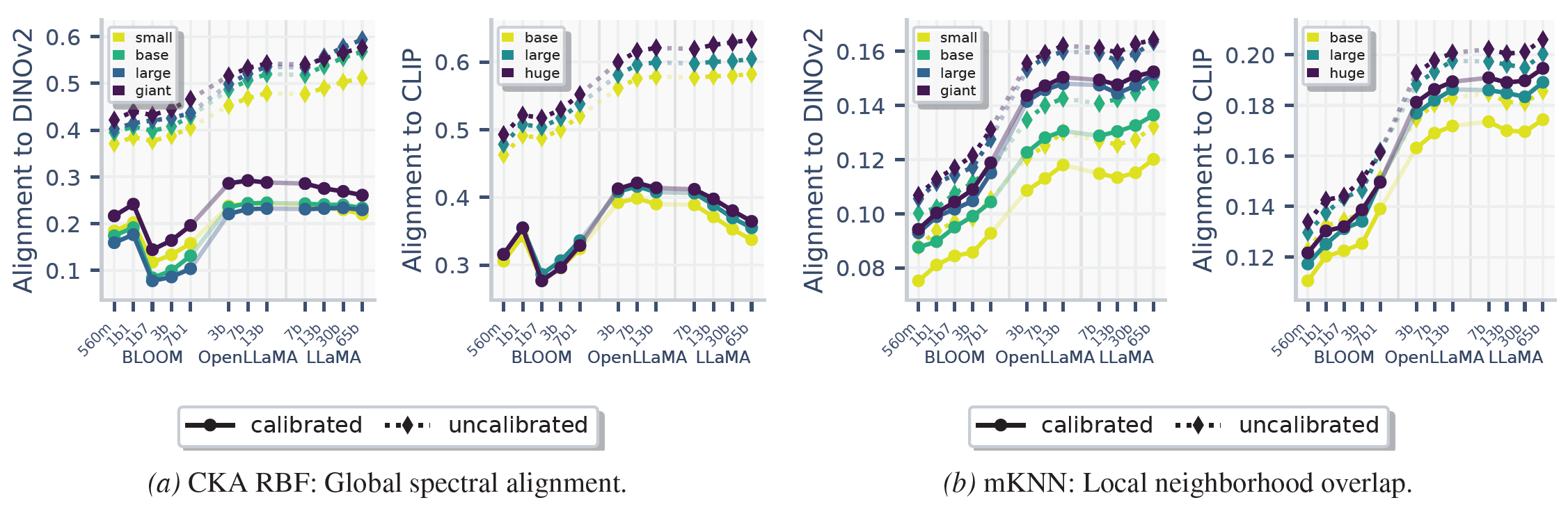
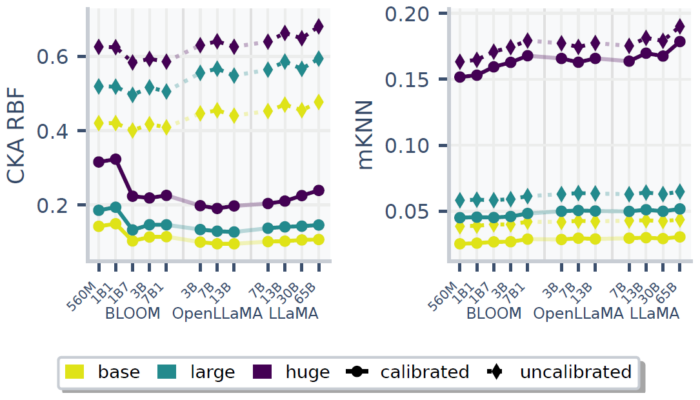
Global spectral similarity (e.g., CKA) largely loses its scaling trend after calibration, suggesting prior “convergence” was driven by width/depth artifacts. In contrast, local neighborhood overlap (e.g., mutual kNN) remains significantly aligned across modalities even after calibration.
We also test video-language alignment and observe the same qualitative pattern: calibrated global similarity shows no systematic scaling trend, while local neighborhood relationships retain a clear scaling signal once representations are sufficiently powerful.
This is why we propose the Aristotelian Representation Hypothesis: models converge in local neighborhood relationships.
Publication
Revisiting the Platonic Representation Hypothesis: An Aristotelian View
Fabian Gröger*, Shuo Wen*, Maria Brbić.
@article{groger2026revisiting,
title = {Revisiting the Platonic Representation Hypothesis: An Aristotelian View},
author = {Gr{\"o}ger, Fabian and Wen, Shuo and Brbi{\'c}, Maria},
journal = {arXiv preprint},
year = {2026},
}
Code
An implementation is available on GitHub.
Contributors
The following people contributed to this work: